Difference between revisions of "Examples/Req"
(→punchline) |
|||
| Line 57: | Line 57: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | + | \frac {R_{1}R_{2}R_{3}R_{4}R_{7}+R_{1}R_{2}R_{3}R_{4}R_{8}+R_{1}R_{2}R_{3}R_{4}R_{11}+R_{1}R_{2}R_{3}R_{6}R_{7}+R_{1}R_{2}R_{3}R_{6}R_{8}+R_{1}R_{2}R_{3}R_{6}R_{11}+R_{1}R_{2}R_{3}R_{7}R_{8}+R_{1}R_{2}R_{3}R_{7}R_{11}+R_{1}R_{2}R_{4}R_{6}R_{7}+R_{1}R_{2}R_{4}R_{6}R_{8}+R_{1}R_{2}R_{4}R_{6}R_{11}+R_{1}R_{2}R_{4}R_{7}R_{8}+R_{1}R_{2}R_{4}R_{7}R_{11}+R_{1}R_{3}R_{4}R_{5}R_{7}+R_{1}R_{3}R_{4}R_{5}R_{8}+R_{1}R_{3}R_{4}R_{5}R_{11}+R_{1}R_{3}R_{4}R_{6}R_{7}+R_{1}R_{3}R_{4}R_{6}R_{8}+R_{1}R_{3}R_{4}R_{6}R_{11}+R_{1}R_{3}R_{4}R_{7}R_{10}+R_{1}R_{3}R_{4}R_{8}R_{10}+R_{1}R_{3}R_{4}R_{10}R_{11}+R_{1}R_{3}R_{5}R_{6}R_{7}+R_{1}R_{3}R_{5}R_{6}R_{8}+R_{1}R_{3}R_{5}R_{6}R_{11}+R_{1}R_{3}R_{5}R_{7}R_{8}+R_{1}R_{3}R_{5}R_{7}R_{11}+R_{1}R_{3}R_{6}R_{7}R_{8}+R_{1}R_{3}R_{6}R_{7}R_{10}+R_{1}R_{3}R_{6}R_{7}R_{11}+R_{1}R_{3}R_{6}R_{8}R_{10}+R_{1}R_{3}R_{6}R_{10}R_{11}+R_{1}R_{3}R_{7}R_{8}R_{10}+R_{1}R_{3}R_{7}R_{10}R_{11}+R_{1}R_{4}R_{5}R_{6}R_{7}+R_{1}R_{4}R_{5}R_{6}R_{8}+R_{1}R_{4}R_{5}R_{6}R_{11}+R_{1}R_{4}R_{5}R_{7}R_{8}+R_{1}R_{4}R_{5}R_{7}R_{11}+R_{1}R_{4}R_{6}R_{7}R_{8}+R_{1}R_{4}R_{6}R_{7}R_{10}+R_{1}R_{4}R_{6}R_{7}R_{11}+R_{1}R_{4}R_{6}R_{8}R_{10}+R_{1}R_{4}R_{6}R_{10}R_{11}+R_{1}R_{4}R_{7}R_{8}R_{10}+R_{1}R_{4}R_{7}R_{10}R_{11}+R_{2}R_{3}R_{4}R_{5}R_{7}+R_{2}R_{3}R_{4}R_{5}R_{8}+R_{2}R_{3}R_{4}R_{5}R_{11}+R_{2}R_{3}R_{4}R_{7}R_{9}+R_{2}R_{3}R_{4}R_{8}R_{9}+R_{2}R_{3}R_{4}R_{9}R_{11}+R_{2}R_{3}R_{5}R_{6}R_{7}+R_{2}R_{3}R_{5}R_{6}R_{8}+R_{2}R_{3}R_{5}R_{6}R_{11}+R_{2}R_{3}R_{5}R_{7}R_{8}+R_{2}R_{3}R_{5}R_{7}R_{11}+R_{2}R_{3}R_{6}R_{7}R_{9}+R_{2}R_{3}R_{6}R_{8}R_{9}+R_{2}R_{3}R_{6}R_{9}R_{11}+R_{2}R_{3}R_{7}R_{8}R_{9}+R_{2}R_{3}R_{7}R_{9}R_{11}+R_{2}R_{4}R_{5}R_{6}R_{7}+R_{2}R_{4}R_{5}R_{6}R_{8}+R_{2}R_{4}R_{5}R_{6}R_{11}+R_{2}R_{4}R_{5}R_{7}R_{8}+R_{2}R_{4}R_{5}R_{7}R_{11}+R_{2}R_{4}R_{6}R_{7}R_{9}+R_{2}R_{4}R_{6}R_{8}R_{9}+R_{2}R_{4}R_{6}R_{9}R_{11}+R_{2}R_{4}R_{7}R_{8}R_{9}+R_{2}R_{4}R_{7}R_{9}R_{11}+R_{3}R_{4}R_{5}R_{6}R_{7}+R_{3}R_{4}R_{5}R_{6}R_{8}+R_{3}R_{4}R_{5}R_{6}R_{11}+R_{3}R_{4}R_{5}R_{7}R_{9}+R_{3}R_{4}R_{5}R_{7}R_{10}+R_{3}R_{4}R_{5}R_{8}R_{9}+R_{3}R_{4}R_{5}R_{8}R_{10}+R_{3}R_{4}R_{5}R_{9}R_{11}+R_{3}R_{4}R_{5}R_{10}R_{11}+R_{3}R_{4}R_{6}R_{7}R_{9}+R_{3}R_{4}R_{6}R_{8}R_{9}+R_{3}R_{4}R_{6}R_{9}R_{11}+R_{3}R_{4}R_{7}R_{9}R_{10}+R_{3}R_{4}R_{8}R_{9}R_{10}+R_{3}R_{4}R_{9}R_{10}R_{11}+R_{3}R_{5}R_{6}R_{7}R_{8}+R_{3}R_{5}R_{6}R_{7}R_{9}+R_{3}R_{5}R_{6}R_{7}R_{10}+R_{3}R_{5}R_{6}R_{7}R_{11}+R_{3}R_{5}R_{6}R_{8}R_{9}+R_{3}R_{5}R_{6}R_{8}R_{10}+R_{3}R_{5}R_{6}R_{9}R_{11}+R_{3}R_{5}R_{6}R_{10}R_{11}+R_{3}R_{5}R_{7}R_{8}R_{9}+R_{3}R_{5}R_{7}R_{8}R_{10}+R_{3}R_{5}R_{7}R_{9}R_{11}+R_{3}R_{5}R_{7}R_{10}R_{11}+R_{3}R_{6}R_{7}R_{8}R_{9}+R_{3}R_{6}R_{7}R_{9}R_{10}+R_{3}R_{6}R_{7}R_{9}R_{11}+R_{3}R_{6}R_{8}R_{9}R_{10}+R_{3}R_{6}R_{9}R_{10}R_{11}+R_{3}R_{7}R_{8}R_{9}R_{10}+R_{3}R_{7}R_{9}R_{10}R_{11}+R_{4}R_{5}R_{6}R_{7}R_{8}+R_{4}R_{5}R_{6}R_{7}R_{9}+R_{4}R_{5}R_{6}R_{7}R_{10}+R_{4}R_{5}R_{6}R_{7}R_{11}+R_{4}R_{5}R_{6}R_{8}R_{9}+R_{4}R_{5}R_{6}R_{8}R_{10}+R_{4}R_{5}R_{6}R_{9}R_{11}+R_{4}R_{5}R_{6}R_{10}R_{11}+R_{4}R_{5}R_{7}R_{8}R_{9}+R_{4}R_{5}R_{7}R_{8}R_{10}+R_{4}R_{5}R_{7}R_{9}R_{11}+R_{4}R_{5}R_{7}R_{10}R_{11}+R_{4}R_{6}R_{7}R_{8}R_{9}+R_{4}R_{6}R_{7}R_{9}R_{10}+R_{4}R_{6}R_{7}R_{9}R_{11}+R_{4}R_{6}R_{8}R_{9}R_{10}+R_{4}R_{6}R_{9}R_{10}R_{11}+R_{4}R_{7}R_{8}R_{9}R_{10}+R_{4}R_{7}R_{9}R_{10}R_{11}}{R_{2}R_{3}R_{4}R_{7}+R_{2}R_{3}R_{4}R_{8}+R_{2}R_{3}R_{4}R_{11}+R_{2}R_{3}R_{6}R_{7}+R_{2}R_{3}R_{6}R_{8}+R_{2}R_{3}R_{6}R_{11}+R_{2}R_{3}R_{7}R_{8}+R_{2}R_{3}R_{7}R_{11}+R_{2}R_{4}R_{6}R_{7}+R_{2}R_{4}R_{6}R_{8}+R_{2}R_{4}R_{6}R_{11}+R_{2}R_{4}R_{7}R_{8}+R_{2}R_{4}R_{7}R_{11}+R_{3}R_{4}R_{5}R_{7}+R_{3}R_{4}R_{5}R_{8}+R_{3}R_{4}R_{5}R_{11}+R_{3}R_{4}R_{6}R_{7}+R_{3}R_{4}R_{6}R_{8}+R_{3}R_{4}R_{6}R_{11}+R_{3}R_{4}R_{7}R_{10}+R_{3}R_{4}R_{8}R_{10}+R_{3}R_{4}R_{10}R_{11}+R_{3}R_{5}R_{6}R_{7}+R_{3}R_{5}R_{6}R_{8}+R_{3}R_{5}R_{6}R_{11}+R_{3}R_{5}R_{7}R_{8}+R_{3}R_{5}R_{7}R_{11}+R_{3}R_{6}R_{7}R_{8}+R_{3}R_{6}R_{7}R_{10}+R_{3}R_{6}R_{7}R_{11}+R_{3}R_{6}R_{8}R_{10}+R_{3}R_{6}R_{10}R_{11}+R_{3}R_{7}R_{8}R_{10}+R_{3}R_{7}R_{10}R_{11}+R_{4}R_{5}R_{6}R_{7}+R_{4}R_{5}R_{6}R_{8}+R_{4}R_{5}R_{6}R_{11}+R_{4}R_{5}R_{7}R_{8}+R_{4}R_{5}R_{7}R_{11}+R_{4}R_{6}R_{7}R_{8}+R_{4}R_{6}R_{7}R_{10}+R_{4}R_{6}R_{7}R_{11}+R_{4}R_{6}R_{8}R_{10}+R_{4}R_{6}R_{10}R_{11}+R_{4}R_{7}R_{8}R_{10}+R_{4}R_{7}R_{10}R_{11}} | |
| − | |||
| − | |||
| − | R_ | ||
| − | 3 | ||
| − | |||
| − | |||
| − | |||
| − | R_ | ||
| − | 1 | ||
| − | |||
| − | |||
| − | |||
| − | }R_ | ||
| − | {7 | ||
| − | R_ | ||
| − | {6 | ||
| − | |||
| − | R_ | ||
| − | |||
| − | |||
| − | +R_ | ||
| − | 11 | ||
| − | }R_ | ||
| − | |||
| − | |||
| − | |||
| − | R_ | ||
| − | 3 | ||
| − | |||
| − | |||
| − | {2 | ||
| − | R_ | ||
| − | |||
| − | {11 | ||
| − | R_ | ||
| − | 8 | ||
| − | |||
| − | |||
| − | {5 | ||
| − | R_ | ||
| − | 4 | ||
| − | R_ | ||
| − | {3 | ||
| − | R_ | ||
| − | 10 | ||
| − | }R_ | ||
| − | 7 | ||
| − | R_ | ||
| − | 6 | ||
| − | }R_ | ||
| − | {5 | ||
| − | |||
| − | |||
| − | }+R_ | ||
| − | |||
| − | 7 | ||
| − | |||
| − | |||
| − | |||
| − | 5 | ||
| − | |||
| − | {4 | ||
| − | R_ | ||
| − | 10 | ||
| − | }R_ | ||
| − | R_ | ||
| − | {2 | ||
| − | |||
| − | 11 | ||
| − | R_ | ||
| − | 7 | ||
| − | R_ | ||
| − | 4 | ||
| − | |||
| − | |||
| − | }R_ | ||
| − | {11 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | R_ | ||
| − | |||
| − | |||
</math> | </math> | ||
</center> | </center> | ||
Revision as of 03:24, 17 September 2019
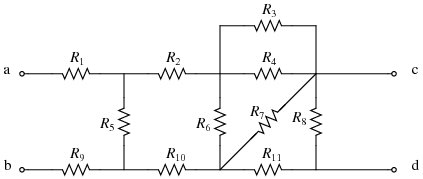
The following shows two step-by-step examples for find the equivalent resistance between two nodes for the following network:
In particular, this example demonstrates how the same network of resistors might reduce differently depending up which two nodes in the network are of interest. Each figure shows the "before" and "after" of a particular step.
\(R_{ab}\!\)
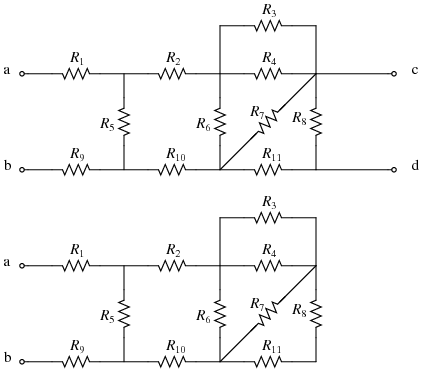
For the first example, we will find the equivalent resistance between nodes a and b.
- Start by focusing only on nodes a and b
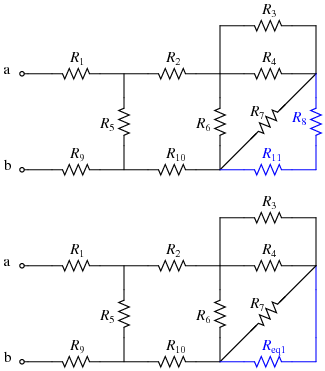
- Next, combine any resistances that are in series. In this particular case, R8 and R11 are now in series because the wire leading to node d has been eliminated. Replace this combination with Req1:
- Since no resistors are currently in series, now look for resistors that are in parallel. R7 and Req1 are in parallel; also, R3 and R4 are in parallel. Replace each with their equivalent resistances (named Req2 and Req3, respectively):
\(R_{eq2}=R_{eq1}||R_7=R_7||(R_8+R_{11})~~~~R_{eq3}=R_3||R_4~~~~\)
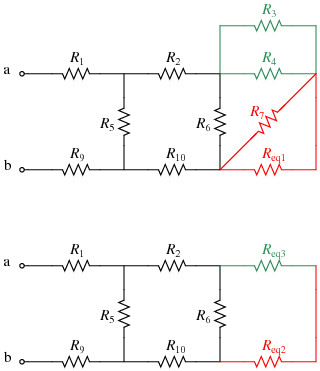
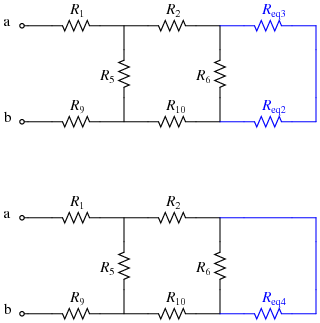
- Now note that Req2 and Req3 are in series; replace them with Req4:
- After that step, R6 and Req4 are in parallel; replace them with Req5:
\(R_{eq5}=R_6||R_{eq4}=R_6||((R_7||(R_8+R_{11}))+(R_3||R_4))\)
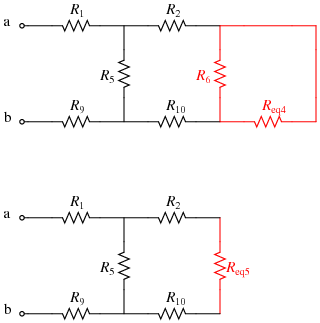
- Next, note that R2, Req5, and R10 are in series; replace them with Req6:
\(R_{eq6}=R_1+R_{eq5}+R_{10}=R_2+(R_6||((R_7||(R_8+R_{11}))+(R_3||R_4)))+R_{10}\)

- Given that network, R5 and Req6 are in parallel; replace them with Req7:
\(R_{eq7}=R_5||R_{eq6}=R_5||(R_2+(R_6||((R_7||(R_8+R_{11}))+(R_3||R_4)))+R_{10}) \)
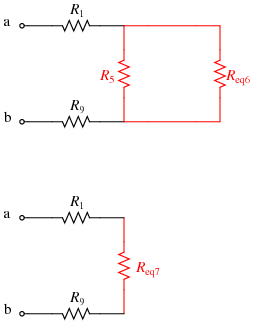
- Finally, R1, Req7, and R9 are in series; replace them with Req,ab, the overall equivalent resistance between nodes a and b:
\(R_{eq,ab}=R_1+R_{eq7}+R_9=R_1+(R_5||(R_2+(R_6||((R_7||(R_8+R_{11}))+(R_3||R_4)))+R_{10}))+R_9\)

- Overall, this yields:
\( R_{eq,ab} = R_1~+~(R_5~||~(R_2~+~(R_6~||~((R_7~||~(R_8~+~R_{11}))+(R_3~||~R_4)))~+~R_{10}))~+~R_9\! \)
or, in other words,
punchline
\( \frac {R_{1}R_{2}R_{3}R_{4}R_{7}+R_{1}R_{2}R_{3}R_{4}R_{8}+R_{1}R_{2}R_{3}R_{4}R_{11}+R_{1}R_{2}R_{3}R_{6}R_{7}+R_{1}R_{2}R_{3}R_{6}R_{8}+R_{1}R_{2}R_{3}R_{6}R_{11}+R_{1}R_{2}R_{3}R_{7}R_{8}+R_{1}R_{2}R_{3}R_{7}R_{11}+R_{1}R_{2}R_{4}R_{6}R_{7}+R_{1}R_{2}R_{4}R_{6}R_{8}+R_{1}R_{2}R_{4}R_{6}R_{11}+R_{1}R_{2}R_{4}R_{7}R_{8}+R_{1}R_{2}R_{4}R_{7}R_{11}+R_{1}R_{3}R_{4}R_{5}R_{7}+R_{1}R_{3}R_{4}R_{5}R_{8}+R_{1}R_{3}R_{4}R_{5}R_{11}+R_{1}R_{3}R_{4}R_{6}R_{7}+R_{1}R_{3}R_{4}R_{6}R_{8}+R_{1}R_{3}R_{4}R_{6}R_{11}+R_{1}R_{3}R_{4}R_{7}R_{10}+R_{1}R_{3}R_{4}R_{8}R_{10}+R_{1}R_{3}R_{4}R_{10}R_{11}+R_{1}R_{3}R_{5}R_{6}R_{7}+R_{1}R_{3}R_{5}R_{6}R_{8}+R_{1}R_{3}R_{5}R_{6}R_{11}+R_{1}R_{3}R_{5}R_{7}R_{8}+R_{1}R_{3}R_{5}R_{7}R_{11}+R_{1}R_{3}R_{6}R_{7}R_{8}+R_{1}R_{3}R_{6}R_{7}R_{10}+R_{1}R_{3}R_{6}R_{7}R_{11}+R_{1}R_{3}R_{6}R_{8}R_{10}+R_{1}R_{3}R_{6}R_{10}R_{11}+R_{1}R_{3}R_{7}R_{8}R_{10}+R_{1}R_{3}R_{7}R_{10}R_{11}+R_{1}R_{4}R_{5}R_{6}R_{7}+R_{1}R_{4}R_{5}R_{6}R_{8}+R_{1}R_{4}R_{5}R_{6}R_{11}+R_{1}R_{4}R_{5}R_{7}R_{8}+R_{1}R_{4}R_{5}R_{7}R_{11}+R_{1}R_{4}R_{6}R_{7}R_{8}+R_{1}R_{4}R_{6}R_{7}R_{10}+R_{1}R_{4}R_{6}R_{7}R_{11}+R_{1}R_{4}R_{6}R_{8}R_{10}+R_{1}R_{4}R_{6}R_{10}R_{11}+R_{1}R_{4}R_{7}R_{8}R_{10}+R_{1}R_{4}R_{7}R_{10}R_{11}+R_{2}R_{3}R_{4}R_{5}R_{7}+R_{2}R_{3}R_{4}R_{5}R_{8}+R_{2}R_{3}R_{4}R_{5}R_{11}+R_{2}R_{3}R_{4}R_{7}R_{9}+R_{2}R_{3}R_{4}R_{8}R_{9}+R_{2}R_{3}R_{4}R_{9}R_{11}+R_{2}R_{3}R_{5}R_{6}R_{7}+R_{2}R_{3}R_{5}R_{6}R_{8}+R_{2}R_{3}R_{5}R_{6}R_{11}+R_{2}R_{3}R_{5}R_{7}R_{8}+R_{2}R_{3}R_{5}R_{7}R_{11}+R_{2}R_{3}R_{6}R_{7}R_{9}+R_{2}R_{3}R_{6}R_{8}R_{9}+R_{2}R_{3}R_{6}R_{9}R_{11}+R_{2}R_{3}R_{7}R_{8}R_{9}+R_{2}R_{3}R_{7}R_{9}R_{11}+R_{2}R_{4}R_{5}R_{6}R_{7}+R_{2}R_{4}R_{5}R_{6}R_{8}+R_{2}R_{4}R_{5}R_{6}R_{11}+R_{2}R_{4}R_{5}R_{7}R_{8}+R_{2}R_{4}R_{5}R_{7}R_{11}+R_{2}R_{4}R_{6}R_{7}R_{9}+R_{2}R_{4}R_{6}R_{8}R_{9}+R_{2}R_{4}R_{6}R_{9}R_{11}+R_{2}R_{4}R_{7}R_{8}R_{9}+R_{2}R_{4}R_{7}R_{9}R_{11}+R_{3}R_{4}R_{5}R_{6}R_{7}+R_{3}R_{4}R_{5}R_{6}R_{8}+R_{3}R_{4}R_{5}R_{6}R_{11}+R_{3}R_{4}R_{5}R_{7}R_{9}+R_{3}R_{4}R_{5}R_{7}R_{10}+R_{3}R_{4}R_{5}R_{8}R_{9}+R_{3}R_{4}R_{5}R_{8}R_{10}+R_{3}R_{4}R_{5}R_{9}R_{11}+R_{3}R_{4}R_{5}R_{10}R_{11}+R_{3}R_{4}R_{6}R_{7}R_{9}+R_{3}R_{4}R_{6}R_{8}R_{9}+R_{3}R_{4}R_{6}R_{9}R_{11}+R_{3}R_{4}R_{7}R_{9}R_{10}+R_{3}R_{4}R_{8}R_{9}R_{10}+R_{3}R_{4}R_{9}R_{10}R_{11}+R_{3}R_{5}R_{6}R_{7}R_{8}+R_{3}R_{5}R_{6}R_{7}R_{9}+R_{3}R_{5}R_{6}R_{7}R_{10}+R_{3}R_{5}R_{6}R_{7}R_{11}+R_{3}R_{5}R_{6}R_{8}R_{9}+R_{3}R_{5}R_{6}R_{8}R_{10}+R_{3}R_{5}R_{6}R_{9}R_{11}+R_{3}R_{5}R_{6}R_{10}R_{11}+R_{3}R_{5}R_{7}R_{8}R_{9}+R_{3}R_{5}R_{7}R_{8}R_{10}+R_{3}R_{5}R_{7}R_{9}R_{11}+R_{3}R_{5}R_{7}R_{10}R_{11}+R_{3}R_{6}R_{7}R_{8}R_{9}+R_{3}R_{6}R_{7}R_{9}R_{10}+R_{3}R_{6}R_{7}R_{9}R_{11}+R_{3}R_{6}R_{8}R_{9}R_{10}+R_{3}R_{6}R_{9}R_{10}R_{11}+R_{3}R_{7}R_{8}R_{9}R_{10}+R_{3}R_{7}R_{9}R_{10}R_{11}+R_{4}R_{5}R_{6}R_{7}R_{8}+R_{4}R_{5}R_{6}R_{7}R_{9}+R_{4}R_{5}R_{6}R_{7}R_{10}+R_{4}R_{5}R_{6}R_{7}R_{11}+R_{4}R_{5}R_{6}R_{8}R_{9}+R_{4}R_{5}R_{6}R_{8}R_{10}+R_{4}R_{5}R_{6}R_{9}R_{11}+R_{4}R_{5}R_{6}R_{10}R_{11}+R_{4}R_{5}R_{7}R_{8}R_{9}+R_{4}R_{5}R_{7}R_{8}R_{10}+R_{4}R_{5}R_{7}R_{9}R_{11}+R_{4}R_{5}R_{7}R_{10}R_{11}+R_{4}R_{6}R_{7}R_{8}R_{9}+R_{4}R_{6}R_{7}R_{9}R_{10}+R_{4}R_{6}R_{7}R_{9}R_{11}+R_{4}R_{6}R_{8}R_{9}R_{10}+R_{4}R_{6}R_{9}R_{10}R_{11}+R_{4}R_{7}R_{8}R_{9}R_{10}+R_{4}R_{7}R_{9}R_{10}R_{11}}{R_{2}R_{3}R_{4}R_{7}+R_{2}R_{3}R_{4}R_{8}+R_{2}R_{3}R_{4}R_{11}+R_{2}R_{3}R_{6}R_{7}+R_{2}R_{3}R_{6}R_{8}+R_{2}R_{3}R_{6}R_{11}+R_{2}R_{3}R_{7}R_{8}+R_{2}R_{3}R_{7}R_{11}+R_{2}R_{4}R_{6}R_{7}+R_{2}R_{4}R_{6}R_{8}+R_{2}R_{4}R_{6}R_{11}+R_{2}R_{4}R_{7}R_{8}+R_{2}R_{4}R_{7}R_{11}+R_{3}R_{4}R_{5}R_{7}+R_{3}R_{4}R_{5}R_{8}+R_{3}R_{4}R_{5}R_{11}+R_{3}R_{4}R_{6}R_{7}+R_{3}R_{4}R_{6}R_{8}+R_{3}R_{4}R_{6}R_{11}+R_{3}R_{4}R_{7}R_{10}+R_{3}R_{4}R_{8}R_{10}+R_{3}R_{4}R_{10}R_{11}+R_{3}R_{5}R_{6}R_{7}+R_{3}R_{5}R_{6}R_{8}+R_{3}R_{5}R_{6}R_{11}+R_{3}R_{5}R_{7}R_{8}+R_{3}R_{5}R_{7}R_{11}+R_{3}R_{6}R_{7}R_{8}+R_{3}R_{6}R_{7}R_{10}+R_{3}R_{6}R_{7}R_{11}+R_{3}R_{6}R_{8}R_{10}+R_{3}R_{6}R_{10}R_{11}+R_{3}R_{7}R_{8}R_{10}+R_{3}R_{7}R_{10}R_{11}+R_{4}R_{5}R_{6}R_{7}+R_{4}R_{5}R_{6}R_{8}+R_{4}R_{5}R_{6}R_{11}+R_{4}R_{5}R_{7}R_{8}+R_{4}R_{5}R_{7}R_{11}+R_{4}R_{6}R_{7}R_{8}+R_{4}R_{6}R_{7}R_{10}+R_{4}R_{6}R_{7}R_{11}+R_{4}R_{6}R_{8}R_{10}+R_{4}R_{6}R_{10}R_{11}+R_{4}R_{7}R_{8}R_{10}+R_{4}R_{7}R_{10}R_{11}} \)
The resistance between nodes \(c\) and \(d\) will be different because of how the resistors appear to the paths between those two nodes. Specifically, the equivalent resistance between those two terminals is:
\( R_{eq,cd} = (((((R_2~+~R_5~+~R_{10})~||~R_6)~+~(R_3~||~R_4))~||~R_7)~+~R_{11})~||~R_8 \)
Note that resistors \(R_1\) and \(R_9\) are not involved in this equivalent.