Difference between revisions of "EGR 103/Concept List Fall 2019"
Jump to navigation
Jump to search
\(
y=e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}
\)
\(
\begin{align}
y_{init}&=1\\
y_{new}&=y_{old}+\frac{x^n}{n!}
\end{align}
\)
(→Lecture 13 - Linear Algebra and Solutions) |
|||
| Line 335: | Line 335: | ||
* Converting equations to a matrix system: | * Converting equations to a matrix system: | ||
** For a certain circuit, conservation equations learned in upper level classes will yield the following two equations: | ** For a certain circuit, conservation equations learned in upper level classes will yield the following two equations: | ||
| − | :: $$ | + | :: $$\begin{align} |
| − | \begin{align} | ||
\frac{v_1-v_s}{R1}+\frac{v_1}{R_2}+\frac{v_1-v_2}{R_3}&=0\\ | \frac{v_1-v_s}{R1}+\frac{v_1}{R_2}+\frac{v_1-v_2}{R_3}&=0\\ | ||
\frac{v_2-v_1}{R_3}+\frac{v_2}{R_4}=0 | \frac{v_2-v_1}{R_3}+\frac{v_2}{R_4}=0 | ||
| − | \end{align} | + | \end{align}$$ |
| + | :* Assuming $$v_s$$ and the $$R_k$$ values are known, to write this as a matrix equation, you need to get $$v_1$$ and $$v_2$$ on the left and everything else on the right: | ||
| + | :: $$\begin{align} | ||
| + | \left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\right)v_1+\left(-\frac{1}{R_3}\right)v_2&=\frac{v_s}{R_1}\\ | ||
| + | \left(-\frac{1}{R_3}\right)v_1+\left(\frac{1}{R_3}+\frac{1}{R_4}\right)v_2&=0 | ||
| + | \end{align}$$ | ||
| + | :* Now you can write this as a matrix equation: | ||
$$ | $$ | ||
| + | \newcommand{\hmatch}{\vphantom{\frac{1_s}{R_1}}} | ||
| + | \begin{align} | ||
| + | \begin{bmatrix} \frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} & -\frac{1}{R_3} \\ -\frac{1}{R_3} & \frac{1}{R_3}+\frac{1}{R_4} | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} \hmatch v_1 \\ \hmatch v_2 \end{bmatrix} | ||
| + | &= | ||
| + | \begin{bmatrix} \frac{v_s}{R_1} \\ 0 \end{bmatrix} | ||
| + | \end{align}$$ | ||
== Lecture 14 - Solution Sweeps, Norms, and Condition Numbers == | == Lecture 14 - Solution Sweeps, Norms, and Condition Numbers == | ||
Revision as of 23:36, 14 October 2019
This page will be used to keep track of the commands and major concepts for each lecture in EGR 103.
Contents
- 1 Lecture 1 - Introduction
- 2 Lecture 2 - Programs and Programming
- 3 Lecture 3 - "Number" Types
- 4 Lecture 4 - Other Types and Functions
- 5 Lecture 5 - Format, Logic, Decisions, and Loops
- 6 Lecture 6 - String Things and Loops
- 7 Lecture 7 - Applications
- 8 Lecture 8 - Taylor Series and Iterative Solutions
- 9 Lecture 9 - Binary and Floating Point Numbers
- 10 Lecture 10 - Monte Carlo Methods
- 11 Lecture 11 - Style, Code Formatters, Docstrings, and More Walking
- 12 Lecture 12 - Arrays and Matrix Representation in Python
- 13 Lecture 13 - Linear Algebra and Solutions
- 14 Lecture 14 - Solution Sweeps, Norms, and Condition Numbers
Lecture 1 - Introduction
- Class web page: EGR 103L; assignments, contact info, readings, etc - see slides on Errata/Notes page
- Sakai page: Sakai 103L page; grades, surveys and tests, some assignment submissions
- CampusWire page: CampusWire 103L page; message board for questions - you need to be in the class and have the access code to subscribe.
Lecture 2 - Programs and Programming
- Seven steps of programming -
- Watch video on Developing an Algorithm
- Watch video on A Seven Step Approach to Solving Programming Problems
- To play with Python:
- Install it on your machine or a public machine: Download
- Quick tour of Python
- Editing window, variable explorer, and console
- You are not expected to remember any of the specifics about how Python stores things or works with them yet!
Lecture 3 - "Number" Types
- Python is a "typed" language - variables have types
- We will use eight types:
- Focus of the day: int, float, and array
- Focus a little later: string, list, tuple
- Focus later: dictionary, set
- int: integers; Python can store these perfectly
- float: floating point numbers - "numbers with decimal points" - Python sometimes has problems
- array
- Requires numpy, usually with
import numpy as np - Organizational unit for storing rectangular arrays of numbers
- Requires numpy, usually with
- Math with "Number" types works the way you expect
- ** * / // % + -
- Relational operators can compare "Number" Types and work the way you expect with True or False as an answer
- < <= == >= > !=
- With arrays, either same size or one is a single value; result will be an array of True and False the same size as the array
- Slices allow us to extract information from an array or put information into an array
- a[0] is the element in a at the start
- a[3] is the element in a three away from the start
- a[:] is all the elements in a because what is really happening is:
- a[start:until] where start is the first index and until is just *past* the last index;
- a[3:7] will return a[3] through a[6] in 4-element array
- a[start:until:increment] will skip indices by increment instead of 1
- To go backwards, a[start:until:-increment] will start at an index and then go backwards until getting at or just past until.
- For 2-D arrays, you can index items with either separate row and column indices or indices separated by commas:
- a[2][3] is the same as a[2, 3]
- Only works for arrays!
Lecture 4 - Other Types and Functions
- Lists are set off with [ ] and entries can be any valid type (including other lists!); entries can be of different types from other entries
- List items can be changed
- Tuples are indicated by commas without square brackets (and are usually shown with parentheses - which are required if trying to make a tuple an entry in a tuple or a list)
- Dictionaries are collections of key : value pairs set off with { }; keys can be any immutable type (int, float, string, tuple) and must be unique; values can be any type and do not need to be unique
- To read more:
- Note! Many of the tutorials below use Python 2 so instead of
print(thing)it showsprint thing - Lists at tutorialspoint
- Tuples at tutorialspoint
- Dictionary at tutorialspoint
- Note! Many of the tutorials below use Python 2 so instead of
- Defined functions can be multiple lines of code and have multiple outputs.
- Four different types of input parameters:
- Required (listed first)
- Named with defaults (second)
- Additional positional arguments ("*args") (third)
- Function will create a tuple containing these items in order
- Additional keyword arguments ("**kwargs") (last)
- Function will create a dictionary of keyword and value pairs
- Function ends when indentation stops or when the function hits a return statement
- Return returns single item as an item of that type; if there are multiple items returned, they are stored in a tuple
- If there is a left side to the function call, it either needs to be a single variable name or a tuple with as many entries as the number of items returned
- Four different types of input parameters:
Lecture 5 - Format, Logic, Decisions, and Loops
- Creating formatted strings using {} and .format() (format strings, standard format specifiers) -- focus was on using e or f for type, minimumwidth.precision, and possibly a + in front to force printing + for positive numbers.
- Also - Format Specification Mini-Language
- Basics of decisions using if...elif...else
- Building a program to check for vowels, consonants, and y
- Bonus material:
- Rhabarberbarbara - now with subtitles!
- Rhabarberbarbara - live recording!
- Lion-Eating Poet in the Stone Den - 施氏食獅史, or Shī Shì shí shī shǐ
- Buffalo$$^8$$
Lecture 6 - String Things and Loops
ordto get numerical value of each characterchrto get character based on integermap(fun, sequence)to apply a function to each item in a sequence- Basics of while loops
- Basics of for loops
- List comprehensions
- [FUNCTION for VAR in SEQUENCE if LOGIC]
- The FUNCTION should return a single thing (though that thing can be a list, tuple, etc)
- The "if LOGIC" part is optional
[k for k in range(3)]creates[0, 1, 2][k**2 for k in range (5, 8)]creates[25, 36, 49][k for k in 'hello' if k<'i']creates['h', 'e'][(k,k**2) for k in range(11) if k%3==2]creates[(2, 4), (5, 25), (8, 64)]
- [FUNCTION for VAR in SEQUENCE if LOGIC]
- Wait - that's the simplified version...here:
- Wait - that's the simplified version...here:
- Want to see Amharic?
list(map(chr, range(4608, 4992)))
- Want to see the Greek alphabet?
for k in range(913,913+25):
print(chr(k), chr(k+32))
Lecture 7 - Applications
- The Price Is Right - Clock Game video demonstration
# tpir.py from class:
import numpy as np
import time
def create_price(low=100, high=1500):
return np.random.randint(low, high+1)
def get_guess():
guess = int(input('Guess: '))
return guess
def check_guess(actual, guess):
if actual > guess:
print('Higher!')
elif actual < guess:
print('Lower!')
if __name__ == '__main__':
#print(create_price(0, 100))
the_price = create_price()
the_guess = get_guess()
start_time = time.clock()
#print(the_guess)
while the_price != the_guess and (time.clock() < start_time+30):
check_guess(the_price, the_guess)
the_guess = get_guess()
if the_price==the_guess:
print('You win!!!!!!!')
else:
print('LOOOOOOOOOOOOOOOSER')
- NATO Phonetic Translator - NATO phonetic alphabet
# nato_trans.py from class:
fread = open('NATO.dat', 'r')
d = {}
for puppies in fread:
#print(puppies) $ if you want to see the whole line
#key = puppies[0]
#value = puppies[:-1]
#d[key] = value
d[puppies[0]] = puppies[:-1]
fread.close()
hamster = input('Word: ').upper()
for kittens in hamster:
#print(d[letter], end=' ')
print(d.get(kittens, 'XXX'), end=' ')
'''
In class - one question was "in cases where there is not a code, can it
return the original value instead of XXX" -- yes:
print(d.get(kittens, kittens))
'''
- Data file we used:
# NATO.dat from class:
Alfa
Bravo
Charlie
Delta
Echo
Foxtrot
Golf
Hotel
India
Juliett
Kilo
Lima
Mike
November
Oscar
Papa
Quebec
Romeo
Sierra
Tango
Uniform
Victor
Whiskey
X-ray
Yankee
Zulu
Lecture 8 - Taylor Series and Iterative Solutions
- Taylor series fundamentals
- Maclaurin series approximation for exponential uses Chapra 4.2 to compute terms in an infinite sum.
- so
- Newton Method for finding square roots uses Chapra 4.2 to iteratively solve using a mathematical map. To find \(y\) where \(y=\sqrt{x}\):
\( \begin{align} y_{init}&=1\\ y_{new}&=\frac{y_{old}+\frac{x}{y_{old}}}{2} \end{align} \) - See Python version of Fig. 4.2 and modified version of 4.2 in the Resources section of Sakai page under Chapra Pythonified
Lecture 9 - Binary and Floating Point Numbers
- Different number systems convey information in different ways.
- Roman Numerals
- Chinese Numbers
- Ndebe Igbo Numbers
- Binary Numbers
- We went through how to convert between decimal and binary
- Kibibytes et al
- "One billion dollars!" may not mean the same thing to different people: Long and Short Scales
- Floats (specifically double precision floats) are stored with a sign bit, 52 fractional bits, and 11 exponent bits. The exponent bits form a code:
- 0 (or 00000000000): the number is either 0 or a denormal
- 2047 (or 11111111111): the number is either infinite or not-a-number
- Others: the power of 2 for scientific notation is 2**(code-1023)
- The largest number is thus just *under* 2**1024 (ends up being (2-2**-52)**1024\(\approx 1.798\times 10^{308}\).
- The smallest normal number (full precision) is 2**(-1022)\(\approx 2.225\times 10^{-308}\).
- The smallest denormal number (only one significant binary digit) is 2**(-1022)/2**53 or 5e-324.
- When adding or subtracting, Python can only operate on the common significant digits - meaning the smaller number will lose precision.
- (1+1e-16)-1=0 and (1+1e-15)-1=1.1102230246251565e-15
- Avoid intermediate calculations that cause problems: if x=1.7e308,
- (x+x)/x is inf
- x/x + x/x is 2.0
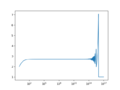
- In cases where mathematical formulas have limits to infinity, you have to pick numbers large enough to properly calculate values but not so large as to cause errors in computing:
- $$e^x=\lim_{n\rightarrow \infty}\left(1+\frac{x}{n}\right)^n$$
# Exponential Demo
<syntaxhighlightlang=python> import numpy as np import matplotlib.pyplot as plt
def exp_calc(x, n):
return (1 + x/n)**n
if __name__ == "__main__":
n = np.logspace(0, 17, 1000)
y = exp_calc(1, n)
fig, ax = plt.subplots(num=1, clear=True)
ax.semilogx(n, y)
fig.savefig('ExpDemoPlot1.png')
# Focus on right part
n = np.logspace(13, 16, 1000)
y = exp_calc(1, n)
fig, ax = plt.subplots(num=2, clear=True)
ax.semilogx(n, y)
fig.savefig('ExpDemoPlot2.png')
</syntaxhighlight>
Lecture 10 - Monte Carlo Methods
- See walk1 in Resources section of Sakai
Lecture 11 - Style, Code Formatters, Docstrings, and More Walking
- Discussion of PEP and PEP8 in particular
- Autostylers include black, autopep8, and yapf -- we will mainly use black
- To get the package:
- On Windows start an Anaconda Prompt (Start->Anaconda3->Anaconda Prompt) or on macOS open a terminal and change to the \users\name\Anaconda3 folder
pip install blackshould install the code
- To use that package:
- Change to the directory where you files lives. On Windows, to change drives, type the driver letter and a colon by itself on a line, then use cd and a path to change directories; on macOS, type
cd /Volumes/NetIDwhere NetID is your NetID to change into your mounted drive. - Type
black FILE.pyand note that this will actually change the file - be sure to save any changes you made to the file before runningblack - As noted in class, black automatically assumes 88 characters in a line; to get it to use the standard 80, use the
-l 80adverb, e.g.black FILE.py -l 80
- Change to the directory where you files lives. On Windows, to change drives, type the driver letter and a colon by itself on a line, then use cd and a path to change directories; on macOS, type
- To get the package:
- Docstrings
- We will be using the numpy style at docstring guide
- Generally need a one-line summary, summary paragraph (if needed), a list of parameters, and a list of returns
- Specific formatting chosen to allow Spyder's built in help tab to format file in a pleasing way
- More walking
- We went through the walk_1 code again and then decided on three different ways we could expand it and looked at how that might impact the code:
- Choose from more integers than just 1 and -1 for the step: very minor impact on code
- Choose from a selection of floating point values: minor impact other than a bit of documentation since ints and floats operate in similar ways
- Walk in 2D rather than along a line: major impact in terms of needing to return x and y value for the step, store x and y value for the location, plot things differently
- All codes from today will be on Sakai in Resources folder
Lecture 12 - Arrays and Matrix Representation in Python
- 1-D and 2-D Arrays
- Python does mathematical operations different for 1 and 2-D arrays
- Matrix multiplication (using @ in Python)
- Setting up linear algebra equations
- Determinants of matrices and the meaning when the determinant is 0
- Shortcuts for determinants of 2x2 and 3x3 matrices
Lecture 13 - Linear Algebra and Solutions
- Converting equations to a matrix system:
- For a certain circuit, conservation equations learned in upper level classes will yield the following two equations:
- $$\begin{align} \frac{v_1-v_s}{R1}+\frac{v_1}{R_2}+\frac{v_1-v_2}{R_3}&=0\\ \frac{v_2-v_1}{R_3}+\frac{v_2}{R_4}=0 \end{align}$$
- Assuming $$v_s$$ and the $$R_k$$ values are known, to write this as a matrix equation, you need to get $$v_1$$ and $$v_2$$ on the left and everything else on the right:
- $$\begin{align} \left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\right)v_1+\left(-\frac{1}{R_3}\right)v_2&=\frac{v_s}{R_1}\\ \left(-\frac{1}{R_3}\right)v_1+\left(\frac{1}{R_3}+\frac{1}{R_4}\right)v_2&=0 \end{align}$$
- Now you can write this as a matrix equation:
$$ \newcommand{\hmatch}{\vphantom{\frac{1_s}{R_1}}} \begin{align} \begin{bmatrix} \frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} & -\frac{1}{R_3} \\ -\frac{1}{R_3} & \frac{1}{R_3}+\frac{1}{R_4} \end{bmatrix} \begin{bmatrix} \hmatch v_1 \\ \hmatch v_2 \end{bmatrix} &= \begin{bmatrix} \frac{v_s}{R_1} \\ 0 \end{bmatrix} \end{align}$$
Lecture 14 - Solution Sweeps, Norms, and Condition Numbers
- See Linear_Algebra#Sweeping_a_Parameter for example code on solving a system of equations when one parameter (either in the coefficient matrix or in the forcing vector or potentially both)