Difference between revisions of "Talk:ECE 280/Spring 2010"
Jump to navigation
Jump to search
m |
|||
| (17 intermediate revisions by 5 users not shown) | |||
| Line 5: | Line 5: | ||
* Here is a sample question - how does Euler's Relationship work for complex exponentials? [[User:DukeEgr93|DukeEgr93]] 17:55, 15 January 2010 (EST) | * Here is a sample question - how does Euler's Relationship work for complex exponentials? [[User:DukeEgr93|DukeEgr93]] 17:55, 15 January 2010 (EST) | ||
** There are a few different ways to show Euler's relationship, one of which involves Taylor/Maclaurin Series Approximations for cos, sin, and e. See [[Complex_Numbers#Euler_Notation| Euler Notation]] on the (as yet not complete - but finished enough for this example) [[Complex Numbers]] page for more detailed information. [[User:DukeEgr93|DukeEgr93]] 17:55, 15 January 2010 (EST) | ** There are a few different ways to show Euler's relationship, one of which involves Taylor/Maclaurin Series Approximations for cos, sin, and e. See [[Complex_Numbers#Euler_Notation| Euler Notation]] on the (as yet not complete - but finished enough for this example) [[Complex Numbers]] page for more detailed information. [[User:DukeEgr93|DukeEgr93]] 17:55, 15 January 2010 (EST) | ||
| + | |||
| + | === Lecture 9 - 2/12 - Discrete Systems === | ||
| + | * From email: Why is<center><math> | ||
| + | x[n] = u[n+2] - u[n-2]\,\!</math></center>the same as<center><math> | ||
| + | x[n] = \delta[n+2] + \delta[n+1] + \delta[n] + \delta[n-1]\,\!</math></center> | ||
| + | ** The main thing here is that for ''discrete'' singularity functions, the impulse function is perfectly defined as having a value of 1 when the argument is zero. What that basically means is:<center><math>u[n-a] = \delta[n-a] + \delta[n-a-1] + \delta[n-a-2] + ...\,\!</math></center>The signal<center><math>x[n]=u[n+2]-u[n-2]\,\!</math></center> is "on" when n=-2, -1, 0, and 1, so it could also be written as a combination of the four delta functions - one for each of those points -<center><math>x[n] = \delta[n+2] + \delta[n+1] + \delta[n] + \delta[n-1]\,\!</math></center>So the x[n] *does* include the n+2 point but *not* the n-2 (because at exactly n-2 the signal turns off). [[User:DukeEgr93|DukeEgr93]] 15:26, 21 February 2010 (EST) | ||
== Questions about particular homework assignments == | == Questions about particular homework assignments == | ||
| Line 28: | Line 34: | ||
** The ''phase'' not not change the periodicity of a signal at all; the phase generally only serves to indicate when a maximum, minimum, or other value happens. [[User:DukeEgr93|DukeEgr93]] 02:02, 17 January 2010 (EST) | ** The ''phase'' not not change the periodicity of a signal at all; the phase generally only serves to indicate when a maximum, minimum, or other value happens. [[User:DukeEgr93|DukeEgr93]] 02:02, 17 January 2010 (EST) | ||
| − | * | + | *On a similar note, does this phase shift affect what exactly the fundamental period would be given two combined signals with different phases? Or is this still irrelevant? [[User:Mdo9|Mdo9]] 02:46, 17 January 2010 (EST) |
** ''Almost'' irrelevant to whether or not the combined signal is periodic and what the period is - with one set of exceptions: complete deconstructive interference. For example, if you are putting together three signals and two of them just happen to cancel each other out, then the period of the overall signal would be the same as the signal that remains. That is to say, if you are looking at <center><math>\begin{align} | ** ''Almost'' irrelevant to whether or not the combined signal is periodic and what the period is - with one set of exceptions: complete deconstructive interference. For example, if you are putting together three signals and two of them just happen to cancel each other out, then the period of the overall signal would be the same as the signal that remains. That is to say, if you are looking at <center><math>\begin{align} | ||
x_1(t)&=\cos(t) & x_2(t)&=\sin(\pi t) & x_3(t)&=\cos(t+\phi) | x_1(t)&=\cos(t) & x_2(t)&=\sin(\pi t) & x_3(t)&=\cos(t+\phi) | ||
| Line 36: | Line 42: | ||
*Part I of HW1 states that we must determine whether a function is periodic or not. Does this mean that we must provide a proof for each function, or can we just state a(t) is periodic with period xx and b(t) is not periodic? [[User:Tbg4|Tbg4]] 16:03, 17 January 2010 (EST)tbg4 | *Part I of HW1 states that we must determine whether a function is periodic or not. Does this mean that we must provide a proof for each function, or can we just state a(t) is periodic with period xx and b(t) is not periodic? [[User:Tbg4|Tbg4]] 16:03, 17 January 2010 (EST)tbg4 | ||
**You do not have to show proof the periodicity, per se, but you should show work in determining what the period is if it is periodic. My fault for not putting enough direction in the problem statement... [[User:DukeEgr93|DukeEgr93]] 18:55, 17 January 2010 (EST) | **You do not have to show proof the periodicity, per se, but you should show work in determining what the period is if it is periodic. My fault for not putting enough direction in the problem statement... [[User:DukeEgr93|DukeEgr93]] 18:55, 17 January 2010 (EST) | ||
| + | |||
| + | *When graphing a function and its respective even and odd parts, these three graphs often overlap in the MATLAB plot and obscure the entire 'picture' of what's going on with all three of the graphs; is there an easy way to fix this? [[User:Mdo9|Mdo9]] 16:53, 18 January 2010 (EST) | ||
| + | ** You can use different line widths, different line styles, or you could use subplot to make three different graphs lined up in a column if that makes the most sense. [[User:DukeEgr93|DukeEgr93]] 17:53, 18 January 2010 (EST) | ||
| + | |||
| + | === Homework 4 === | ||
| + | |||
| + | * For Part II b, what is the "desired data", how is it related to the input step function accumulation signal, and how does comparing it to the step response tell you something useful? [[ehs10]] 09:21, 15 February 2010 (EST) | ||
| + | ** "Desired data" will be the sets of 1 and -1 that represents the two different binary signals you are trying to transmit. The step response of the circuit will be useful because the input - which is the same as the desired signal - will be a linear combination of scaled and shifted step functions; this means that the output will be the same linear combination of shifted and scaled step responses. [[User:DukeEgr93|DukeEgr93]] 10:04, 15 February 2010 (EST) | ||
== Questions about particular labs == | == Questions about particular labs == | ||
| + | === Lab 4 === | ||
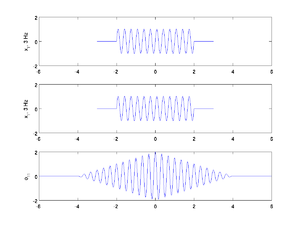
| + | *In Lab 4-Touch Tone Phone System, we don't completely understand what the correlation plots are telling us. Our thinking is that the dual-tone signal will obviously correlate most with the sinusoids it is composed of. The graphs of high correlation are diamond shaped, and we think this is the case because correlation involves a convolution, and so as one signal moves past another in the convolution, the integral over the combined area will increase then decrease after the point when the signals are on top of eachother. When zooming into the plots we see they are sinusoidal--does this mean the area is becoming positive then negative? Thanks! [[User:Jtk11|Jtk11]] 21:20, 24 March 2010 (EDT) | ||
| + | ** [[File:CorrDemo phi11.png|thumb|Correlation of two signals at 3 Hz]][[File:CorrDemo phi12.png|thumb|Correlation of signals at 3 Hz and 4 Hz]]Imagine doing the correlation of two signals that each have windows containing a sinusoid of the same frequency; when one of the signals is shifted the the "right place" - i.e. the sinusoids perfectly overlap, the product of those two will be an integrand that is always positive and you will get as large a value for the correlation as possible - that's the peak. As they slide past each other more, however, you will get to a spot where they are 180 degrees out of phase. At that point, the integrand is made up of a completely '''negative''' product and the correlation will be a large negative number. Keep sliding, and the signals will mostly line up again (yay!) and then get completely out again (boo!). All of which is to say, when doing the correlation of two signals with windows having the same sinusoid in them, you should expect a decaying sinusoid as the correlation with the best relative time shift between the two indicated by the primary peak of the correlation. There are examples of both these situations at right. [[User:DukeEgr93|DukeEgr93]] 21:49, 24 March 2010 (EDT) | ||
| − | + | <br clear=all/> | |
== General questions == | == General questions == | ||
*I can't find a working link for xwin. [[User:Tbg4|Tbg4]] 18:07, 17 January 2010 (EST)tbg4 | *I can't find a working link for xwin. [[User:Tbg4|Tbg4]] 18:07, 17 January 2010 (EST)tbg4 | ||
** [[X-Win]]? Which links were broken? [[User:DukeEgr93|DukeEgr93]] 18:55, 17 January 2010 (EST) | ** [[X-Win]]? Which links were broken? [[User:DukeEgr93|DukeEgr93]] 18:55, 17 January 2010 (EST) | ||
| + | *** The download/registration links. I found it here - http://www.oit.duke.edu/comp-print/software/license/index.php - there a lot of old direct links off of google and some duke sites which are dead. [[User:Tbg4|Tbg4]] 17:11, 18 January 2010 (EST)tbg4 | ||
| + | **** A-ha - I try to put those links in the software box at the top right of the page; the one that is in [[X-Win]] works for me. [[User:DukeEgr93|DukeEgr93]] 17:53, 18 January 2010 (EST) | ||
| + | *Rather a MATLAB question: I SSH'd into login1.oit.duke.edu and got Matlab started, but when I give it the sound(y,Fs) command it tells me: | ||
| + | <source lang="bash"> | ||
| + | ??? Error using ==> playsnd at 18 | ||
| + | The requested audio format is not supported | ||
| + | |||
| + | Error in ==> sound at 46 | ||
| + | playsnd(y,fs,bits); </source> | ||
| + | :Is this a prob with my computer or with SSH-ing into a different computer? -ehs10 | ||
| + | :* That's actually an issue with trying to play audio through x-win. Unfortunately, you can only play audio on MATLAB at the computer where MATLAB is running, so if you want to hear sounds, you need to be sitting in Hudson or Teer or in the ECE 280 lab. [[User:DukeEgr93|DukeEgr93]] 17:58, 19 January 2010 (EST) | ||
Latest revision as of 19:36, 1 June 2013
When posting questions, please be sure to use the Q Template so the instructor and TAs will see the question. Note in the examples below the Q Template has been removed to indicate that the question has been answered.
Contents
Questions about particular lectures
Lecture 2 - 1/15
- Here is a sample question - how does Euler's Relationship work for complex exponentials? DukeEgr93 17:55, 15 January 2010 (EST)
- There are a few different ways to show Euler's relationship, one of which involves Taylor/Maclaurin Series Approximations for cos, sin, and e. See Euler Notation on the (as yet not complete - but finished enough for this example) Complex Numbers page for more detailed information. DukeEgr93 17:55, 15 January 2010 (EST)
Lecture 9 - 2/12 - Discrete Systems
- From email: Why is
\( x[n] = u[n+2] - u[n-2]\,\!\) the same as\( x[n] = \delta[n+2] + \delta[n+1] + \delta[n] + \delta[n-1]\,\!\) - The main thing here is that for discrete singularity functions, the impulse function is perfectly defined as having a value of 1 when the argument is zero. What that basically means is:
\(u[n-a] = \delta[n-a] + \delta[n-a-1] + \delta[n-a-2] + ...\,\!\) The signal\(x[n]=u[n+2]-u[n-2]\,\!\) is "on" when n=-2, -1, 0, and 1, so it could also be written as a combination of the four delta functions - one for each of those points -\(x[n] = \delta[n+2] + \delta[n+1] + \delta[n] + \delta[n-1]\,\!\) So the x[n] *does* include the n+2 point but *not* the n-2 (because at exactly n-2 the signal turns off). DukeEgr93 15:26, 21 February 2010 (EST)
- The main thing here is that for discrete singularity functions, the impulse function is perfectly defined as having a value of 1 when the argument is zero. What that basically means is:
Questions about particular homework assignments
Homework 1
- Here is a sample question - how do I get access to the code from class that seems really relevant to this assignment? DukeEgr93 17:55, 15 January 2010 (EST)
- All codes written in class will go in my ~mrg/ECE54 folder with each day having its own folder. If you use code developed in class. be sure that the comments section at the top of the code indicates that the code is a modified form of my code. Something on the order of:
% [Function or Script Name]
% [Your Name]
% [Date Written]
% Based in part on:
% [Original Function or Script Name]
% [Original author name]
% Accessed on: [Date accessed]
% With my NET ID as a signature, I hereby indicate that I understand and
% have followed the Duke Community Standard in completing this assignment
% Signed: [Your NET ID]
- should work. DukeEgr93 17:55, 15 January 2010 (EST)
- When deciding whether a signal is periodic or not, does the phase shift factor in at all? Mdo9 20:06, 16 January 2010 (EST)
- The phase not not change the periodicity of a signal at all; the phase generally only serves to indicate when a maximum, minimum, or other value happens. DukeEgr93 02:02, 17 January 2010 (EST)
- On a similar note, does this phase shift affect what exactly the fundamental period would be given two combined signals with different phases? Or is this still irrelevant? Mdo9 02:46, 17 January 2010 (EST)
- Almost irrelevant to whether or not the combined signal is periodic and what the period is - with one set of exceptions: complete deconstructive interference. For example, if you are putting together three signals and two of them just happen to cancel each other out, then the period of the overall signal would be the same as the signal that remains. That is to say, if you are looking at
\(\begin{align} x_1(t)&=\cos(t) & x_2(t)&=\sin(\pi t) & x_3(t)&=\cos(t+\phi) \end{align}\) and trying to determine if\(\begin{align} y(t)&=x_1(t)+x_2(t)+x_3(t) \end{align}\) is periodic, then for most values of \(\phi\) the signal \(y(t)\) will not be periodic since the component periods do not form rational fractions. However, if \(\phi\) happens to be \(\pi\) rad (or some angular equivalent to it), then \(x_1(t)\) and \(x_3(t)\) would cancel out, leaving just \(x_2(t)\) and in that specific instance, \(y(t)\) would be a periodic signal with period \(T=2\) sec.Otherwise, however, the phase does not have an impact on whether a combined signal is period and, if it is, on what the period of a combined signal would be. DukeEgr93 09:24, 17 January 2010 (EST)
- Almost irrelevant to whether or not the combined signal is periodic and what the period is - with one set of exceptions: complete deconstructive interference. For example, if you are putting together three signals and two of them just happen to cancel each other out, then the period of the overall signal would be the same as the signal that remains. That is to say, if you are looking at
- Part I of HW1 states that we must determine whether a function is periodic or not. Does this mean that we must provide a proof for each function, or can we just state a(t) is periodic with period xx and b(t) is not periodic? Tbg4 16:03, 17 January 2010 (EST)tbg4
- You do not have to show proof the periodicity, per se, but you should show work in determining what the period is if it is periodic. My fault for not putting enough direction in the problem statement... DukeEgr93 18:55, 17 January 2010 (EST)
- When graphing a function and its respective even and odd parts, these three graphs often overlap in the MATLAB plot and obscure the entire 'picture' of what's going on with all three of the graphs; is there an easy way to fix this? Mdo9 16:53, 18 January 2010 (EST)
- You can use different line widths, different line styles, or you could use subplot to make three different graphs lined up in a column if that makes the most sense. DukeEgr93 17:53, 18 January 2010 (EST)
Homework 4
- For Part II b, what is the "desired data", how is it related to the input step function accumulation signal, and how does comparing it to the step response tell you something useful? ehs10 09:21, 15 February 2010 (EST)
- "Desired data" will be the sets of 1 and -1 that represents the two different binary signals you are trying to transmit. The step response of the circuit will be useful because the input - which is the same as the desired signal - will be a linear combination of scaled and shifted step functions; this means that the output will be the same linear combination of shifted and scaled step responses. DukeEgr93 10:04, 15 February 2010 (EST)
Questions about particular labs
Lab 4
- In Lab 4-Touch Tone Phone System, we don't completely understand what the correlation plots are telling us. Our thinking is that the dual-tone signal will obviously correlate most with the sinusoids it is composed of. The graphs of high correlation are diamond shaped, and we think this is the case because correlation involves a convolution, and so as one signal moves past another in the convolution, the integral over the combined area will increase then decrease after the point when the signals are on top of eachother. When zooming into the plots we see they are sinusoidal--does this mean the area is becoming positive then negative? Thanks! Jtk11 21:20, 24 March 2010 (EDT)
- Imagine doing the correlation of two signals that each have windows containing a sinusoid of the same frequency; when one of the signals is shifted the the "right place" - i.e. the sinusoids perfectly overlap, the product of those two will be an integrand that is always positive and you will get as large a value for the correlation as possible - that's the peak. As they slide past each other more, however, you will get to a spot where they are 180 degrees out of phase. At that point, the integrand is made up of a completely negative product and the correlation will be a large negative number. Keep sliding, and the signals will mostly line up again (yay!) and then get completely out again (boo!). All of which is to say, when doing the correlation of two signals with windows having the same sinusoid in them, you should expect a decaying sinusoid as the correlation with the best relative time shift between the two indicated by the primary peak of the correlation. There are examples of both these situations at right. DukeEgr93 21:49, 24 March 2010 (EDT)
General questions
- I can't find a working link for xwin. Tbg4 18:07, 17 January 2010 (EST)tbg4
- X-Win? Which links were broken? DukeEgr93 18:55, 17 January 2010 (EST)
- The download/registration links. I found it here - http://www.oit.duke.edu/comp-print/software/license/index.php - there a lot of old direct links off of google and some duke sites which are dead. Tbg4 17:11, 18 January 2010 (EST)tbg4
- X-Win? Which links were broken? DukeEgr93 18:55, 17 January 2010 (EST)
- Rather a MATLAB question: I SSH'd into login1.oit.duke.edu and got Matlab started, but when I give it the sound(y,Fs) command it tells me:
??? Error using ==> playsnd at 18
The requested audio format is not supported
Error in ==> sound at 46
playsnd(y,fs,bits);
- Is this a prob with my computer or with SSH-ing into a different computer? -ehs10
- That's actually an issue with trying to play audio through x-win. Unfortunately, you can only play audio on MATLAB at the computer where MATLAB is running, so if you want to hear sounds, you need to be sitting in Hudson or Teer or in the ECE 280 lab. DukeEgr93 17:58, 19 January 2010 (EST)