Difference between revisions of "Symbolic/Examples/Circuits"
(→Python) |
(→Maple) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | == Counting Equations == | ||
| + | For an electric circuit containing only wires, sources, and resistances, three primary kinds of equations will help solve for the individual voltages and currents that may exist in the circuit. These are element equations, Kirchhoff's Current Law (KCL), and Kirchhoff's Voltage Law (KVL). | ||
| − | == Brute Force | + | With respect to element equations, these can take multiple forms. For independent sources, the element equation is generally a value assigned to the source. For example, if there is a 10 V voltage source in the circuit, the element equation would be that the voltage across that element is 10 V. For resistances, the element equation is generally Ohm's Law |
| − | The following example shows the "brute force" method of setting up and solving for all the element currents and voltages for a simple resistive circuit and then using those solutions to solve for auxiliary information (in this case, some powers). The circuit involved is: | + | <center><math> |
| + | \begin{align*} | ||
| + | v=iR | ||
| + | \end{align*} | ||
| + | </math></center> | ||
| + | so long as the voltage and current are labeled using the passive sign convention. Finally, for dependent sources, the element equation will relate a voltage or current in the circuit to the dependent variable of the source. There will be as many element equations as there are elements, though typically independent source values are counted as "knowns" rather than "element equations." | ||
| + | |||
| + | For Kirchhoff's Current Law, the number of independent equations that can be generated by applying it will be one fewer than the number of nodes in the circuit. Note that this does not explicitly mean that KCL must only be applied at simple nodes - "supernodes" which combine multiple nodes may also be used, though care must be taken to make sure the combination of equations constitutes an independent set. Furthermore, there will be times when you might split a node into parts to determine currents flowing through specific wires that make up the node. For the brute force method, we will use simple nodes. | ||
| + | |||
| + | For Kirchhoff's Voltage Law, the number of independent equations that can be derived in a circuit consisting solely of two-terminal elements will be equal to:<ref name="Feldmann">Peter Feldmann and Ronald A. Rohrer, "Proof of the Number of Independent Kirchhoff Equations in an Electrical Circuit." http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=00135739</ref> | ||
| + | <center><math> | ||
| + | \begin{align*} | ||
| + | \mbox{KVL equations}=\mbox{elements}-\mbox{nodes}+1 | ||
| + | \end{align*} | ||
| + | </math></center> | ||
| + | For planar circuits, this will be equal to the number of meshes in the circuit. There may be times when it is more efficient to use some superloop equations versus mesh equations, but for the brute force method with a planar circuit, we will use mesh equations. | ||
| + | |||
| + | |||
| + | $$\newcommand{\E}[2]{#1_{\mathrm{#2}}}$$ | ||
| + | == Brute Force == | ||
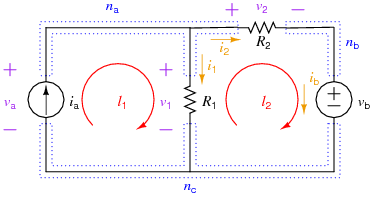
| + | The following example shows the "brute force" method of setting up and solving for all the element currents and voltages for a simple resistive circuit and then using those solutions to solve for auxiliary information (in this case, some powers). The circuit involved, including all labels for element voltages, element currents, nodes, and loops is: | ||
<center> | <center> | ||
[[File:ExCirLabel.png]] | [[File:ExCirLabel.png]] | ||
</center> | </center> | ||
| + | Given that there are four elements, there are a total of eight potential unknowns - four element voltages and four element currents. There are four elements and three nodes, meaning the number and type of equations we can use is: | ||
| + | * 4 elements $$\rightarrow$$ 4 element equations | ||
| + | * 3 nodes - 1 $$\rightarrow$$ 2 independent KCL equations | ||
| + | * 4 elements - 3 nodes + 1 $$\rightarrow$$ 2 independent KVL equations (also, this circuit is planar, so 2 meshes $$\rightarrow$$ 2 independent KVL equations) | ||
| + | Given the two independent sources, it is likely that the "element equations" for those two items will instead be replaced with known values for the current source's current and the voltage source's voltage. That leaves six equations and six unknowns. | ||
=== Equations === | === Equations === | ||
==== Element Equations ==== | ==== Element Equations ==== | ||
Mainly, these are Ohm's Law equations for the resistors, so: | Mainly, these are Ohm's Law equations for the resistors, so: | ||
<center><math> | <center><math> | ||
| − | \begin{align} | + | \begin{align*} |
R_1:& & v_1&=i_1R_1\\ | R_1:& & v_1&=i_1R_1\\ | ||
R_2:& & v_2&=i_2R_2 | R_2:& & v_2&=i_2R_2 | ||
| − | \end{align} | + | \end{align*} |
</math></center> | </math></center> | ||
==== KCL Equations ==== | ==== KCL Equations ==== | ||
| − | The number of independent KCL equations | + | The number of independent KCL equations is one less than the number of nodes, so in this case, 2. ''Note:'' all three nodal KCL equations are written below, but node <math>n_c</math>'s is not used. |
<center><math> | <center><math> | ||
| − | \begin{align} | + | \begin{align*} |
KCL,n_a:& & -i_a+i_1+i_2&=0\\ | KCL,n_a:& & -i_a+i_1+i_2&=0\\ | ||
KCL,n_b:& & -i_2+i_b&=0\\ | KCL,n_b:& & -i_2+i_b&=0\\ | ||
KCL,n_c:& & i_a-i_1-i_b&=0 | KCL,n_c:& & i_a-i_1-i_b&=0 | ||
| − | \end{align} | + | \end{align*} |
</math></center> | </math></center> | ||
| + | Note that the equation for node $$c$$ is equal and opposite to the sum of the equations for nodes $$a$$ and $$b$$ together. | ||
==== KVL Equations ==== | ==== KVL Equations ==== | ||
The number of independent KVL equations is equal to the number of meshes for a 2-D circuit, or to the number of elements, minus the number of nodes, plus one for circuits in general. In this case, that is 2 independent KVL (two meshes, or 3 elements - 3 nodes + 1 = 2). For the brute force method, just use the mesh equations: | The number of independent KVL equations is equal to the number of meshes for a 2-D circuit, or to the number of elements, minus the number of nodes, plus one for circuits in general. In this case, that is 2 independent KVL (two meshes, or 3 elements - 3 nodes + 1 = 2). For the brute force method, just use the mesh equations: | ||
<center><math> | <center><math> | ||
| − | \begin{align} | + | \begin{align*} |
KVL,l_1:& & -v_a+v_1&=0\\ | KVL,l_1:& & -v_a+v_1&=0\\ | ||
KVL,l_2:& & -v_1+v_2+v_b&=0 | KVL,l_2:& & -v_1+v_2+v_b&=0 | ||
| − | \end{align} | + | \end{align*} |
</math></center> | </math></center> | ||
| + | You can check this by writing the KVL equation for the superloop | ||
| + | <center><math> | ||
| + | \begin{align*} | ||
| + | KVL,sl_{12}:& & -v_a+v_2+v_b&=0\\ | ||
| + | \end{align*} | ||
| + | </math></center> | ||
| + | and then noting that this equation is the sum of the equations for the two component meshes. | ||
==== Auxiliary Equations ==== | ==== Auxiliary Equations ==== | ||
For this example, the auxiliary equations will be used to determine the power delivered by each source and the power absorbed by each resistor: | For this example, the auxiliary equations will be used to determine the power delivered by each source and the power absorbed by each resistor: | ||
<center><math> | <center><math> | ||
| − | \begin{align} | + | \begin{align*} |
p_{del,i_a}&=v_ai_a & p_{del,v_b}&=-v_bi_b \\ | p_{del,i_a}&=v_ai_a & p_{del,v_b}&=-v_bi_b \\ | ||
p_{abs,R_1}&=v_1i_1 & p_{abs,R_2}&=v_2i_2 | p_{abs,R_1}&=v_1i_1 & p_{abs,R_2}&=v_2i_2 | ||
| − | \end{align} | + | \end{align*} |
</math></center> | </math></center> | ||
Note that all elements except for <math>i_a</math> are labeled passively. | Note that all elements except for <math>i_a</math> are labeled passively. | ||
| + | ==== Summary of Equations ==== | ||
| + | At this stage, there are a total of six unknowns: $$\E{v}{a}$$, | ||
| + | $$\E{v}{1}$$, $$\E{v}{2}$$, $$\E{i}{b}$$, $$\E{i}{1}$$, and $$\E{i}{2}$$. | ||
| + | This requires six independent equations. From the three sections above, we have: | ||
| + | <center><math> | ||
| + | \begin{align*} | ||
| + | ~&\mbox{Ohm's Law, }\E{R}{1}:&\E{v}{1}&=\E{i}{1}\E{R}{1}\\ | ||
| + | ~&\mbox{Ohm's Law, }\E{R}{2}:&\E{v}{2}&=\E{i}{2}\E{R}{2}\\ | ||
| + | ~&\mbox{KCL, }\E{n}{a}:&-\E{i}{a}+\E{i}{1}+\E{i}{2}&=0\\ | ||
| + | ~&\mbox{KCL, }\E{n}{b}:&-\E{i}{2}+\E{i}{b}&=0\\ | ||
| + | ~&\mbox{KVL, }\E{l}{1}:&-\E{v}{a}+\E{v}{1}&=0\\ | ||
| + | ~&\mbox{KVL, }\E{l}{2}:&-\E{v}{1}+\E{v}{2}+\E{v}{b}&=0\\ | ||
| + | \end{align*} | ||
| + | </math></center> | ||
| + | |||
| + | === Matrix Version === | ||
| + | Once you have found the necessary equations, there are multiple methods for solving them. If you choose to use matrix methods, you will need to organize the equations such that all the unknowns (and their coefficients) are on one side and the known items are on the other. You can then set up and solve a matrix equation using whatever method you like (Cramer's Rule, Gaussian Elimination, etc.). For the six equations above, this would yield: | ||
| + | <center><math> | ||
| + | \begin{align*} | ||
| + | \E{v}{1}-\E{i}{1}\E{R}{1}&=0\\ | ||
| + | \E{v}{2}-\E{i}{2}\E{R}{2}&=0\\ | ||
| + | \E{i}{1}+\E{i}{2}&=\E{i}{a}\\ | ||
| + | \E{i}{b}-\E{i}{2}&=0\\ | ||
| + | \E{v}{a}-\E{v}{1}&=0\\ | ||
| + | \E{v}{1}-\E{v}{2}&=\E{v}{b}\\ | ||
| + | \end{align*} | ||
| + | </math></center> | ||
| + | which, in matrix form, becomes: | ||
| + | <center><math> | ||
| + | \begin{align*} | ||
| + | \begin{bmatrix} | ||
| + | 0 & 1 & 0 & 0 & -\E{R}{1} & 0 \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & -\E{R}{2}\\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 1\\ | ||
| + | 0 & 0 & 0 & 1 & 0 & -1\\ | ||
| + | 1 & -1 & 0 & 0 & 0 & 0\\ | ||
| + | 0 & 1 & -1 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | \E{v}{a}\\ \E{v}{1} \\ \E{v}{2} \\ | ||
| + | \E{i}{b}\\ \E{i}{1} \\ \E{i}{2} | ||
| + | \end{bmatrix}&= | ||
| + | \begin{bmatrix} | ||
| + | 0\\ 0\\ \E{i}{a}\\ 0\\ 0\\ \E{v}{b} | ||
| + | \end{bmatrix} | ||
| + | \end{align*} | ||
| + | </math></center> | ||
| + | |||
| + | If you have access to a computer, however, you may consider using a computational tool to do the algebra for you. | ||
| + | |||
=== Code === | === Code === | ||
==== Maple ==== | ==== Maple ==== | ||
| + | Take a look at the [[Maple/Simultaneous Equations]] page first, then come back here. | ||
The Maple worksheet for this example is available in the Maple Cloud at this [https://maple.cloud/app/5433531920023552/Circuit1Demo Maple Cloud Link]. You can view the worksheet even if you do not have Maple; if you have Maple, you can download the worksheet and edit it. | The Maple worksheet for this example is available in the Maple Cloud at this [https://maple.cloud/app/5433531920023552/Circuit1Demo Maple Cloud Link]. You can view the worksheet even if you do not have Maple; if you have Maple, you can download the worksheet and edit it. | ||
Latest revision as of 02:17, 22 January 2024
Contents
Counting Equations
For an electric circuit containing only wires, sources, and resistances, three primary kinds of equations will help solve for the individual voltages and currents that may exist in the circuit. These are element equations, Kirchhoff's Current Law (KCL), and Kirchhoff's Voltage Law (KVL).
With respect to element equations, these can take multiple forms. For independent sources, the element equation is generally a value assigned to the source. For example, if there is a 10 V voltage source in the circuit, the element equation would be that the voltage across that element is 10 V. For resistances, the element equation is generally Ohm's Law
so long as the voltage and current are labeled using the passive sign convention. Finally, for dependent sources, the element equation will relate a voltage or current in the circuit to the dependent variable of the source. There will be as many element equations as there are elements, though typically independent source values are counted as "knowns" rather than "element equations."
For Kirchhoff's Current Law, the number of independent equations that can be generated by applying it will be one fewer than the number of nodes in the circuit. Note that this does not explicitly mean that KCL must only be applied at simple nodes - "supernodes" which combine multiple nodes may also be used, though care must be taken to make sure the combination of equations constitutes an independent set. Furthermore, there will be times when you might split a node into parts to determine currents flowing through specific wires that make up the node. For the brute force method, we will use simple nodes.
For Kirchhoff's Voltage Law, the number of independent equations that can be derived in a circuit consisting solely of two-terminal elements will be equal to:[1]
For planar circuits, this will be equal to the number of meshes in the circuit. There may be times when it is more efficient to use some superloop equations versus mesh equations, but for the brute force method with a planar circuit, we will use mesh equations.
$$\newcommand{\E}[2]{#1_{\mathrm{#2}}}$$
Brute Force
The following example shows the "brute force" method of setting up and solving for all the element currents and voltages for a simple resistive circuit and then using those solutions to solve for auxiliary information (in this case, some powers). The circuit involved, including all labels for element voltages, element currents, nodes, and loops is:
Given that there are four elements, there are a total of eight potential unknowns - four element voltages and four element currents. There are four elements and three nodes, meaning the number and type of equations we can use is:
- 4 elements $$\rightarrow$$ 4 element equations
- 3 nodes - 1 $$\rightarrow$$ 2 independent KCL equations
- 4 elements - 3 nodes + 1 $$\rightarrow$$ 2 independent KVL equations (also, this circuit is planar, so 2 meshes $$\rightarrow$$ 2 independent KVL equations)
Given the two independent sources, it is likely that the "element equations" for those two items will instead be replaced with known values for the current source's current and the voltage source's voltage. That leaves six equations and six unknowns.
Equations
Element Equations
Mainly, these are Ohm's Law equations for the resistors, so:
KCL Equations
The number of independent KCL equations is one less than the number of nodes, so in this case, 2. Note: all three nodal KCL equations are written below, but node \(n_c\)'s is not used.
Note that the equation for node $$c$$ is equal and opposite to the sum of the equations for nodes $$a$$ and $$b$$ together.
KVL Equations
The number of independent KVL equations is equal to the number of meshes for a 2-D circuit, or to the number of elements, minus the number of nodes, plus one for circuits in general. In this case, that is 2 independent KVL (two meshes, or 3 elements - 3 nodes + 1 = 2). For the brute force method, just use the mesh equations:
You can check this by writing the KVL equation for the superloop
and then noting that this equation is the sum of the equations for the two component meshes.
Auxiliary Equations
For this example, the auxiliary equations will be used to determine the power delivered by each source and the power absorbed by each resistor:
Note that all elements except for \(i_a\) are labeled passively.
Summary of Equations
At this stage, there are a total of six unknowns: $$\E{v}{a}$$, $$\E{v}{1}$$, $$\E{v}{2}$$, $$\E{i}{b}$$, $$\E{i}{1}$$, and $$\E{i}{2}$$. This requires six independent equations. From the three sections above, we have:
Matrix Version
Once you have found the necessary equations, there are multiple methods for solving them. If you choose to use matrix methods, you will need to organize the equations such that all the unknowns (and their coefficients) are on one side and the known items are on the other. You can then set up and solve a matrix equation using whatever method you like (Cramer's Rule, Gaussian Elimination, etc.). For the six equations above, this would yield:
which, in matrix form, becomes:
If you have access to a computer, however, you may consider using a computational tool to do the algebra for you.
Code
Maple
Take a look at the Maple/Simultaneous Equations page first, then come back here. The Maple worksheet for this example is available in the Maple Cloud at this Maple Cloud Link. You can view the worksheet even if you do not have Maple; if you have Maple, you can download the worksheet and edit it.
The code assumes that:
Python
Starting in 2022, we are looking at using Python to perform symbolic calculations. You can view three Notebook forms on a Google Drive Folder that has three versions of the example:
- "nosub" uses no subscripts for the variables; SymPy will automatically make variables with single digits at the end print with subscripts (like $$i_1$$) but will not do subscripts for things like $$ia$$
- "allsub" uses subscripts for all the variables - which requires also putting the subscripts in the code
- "dispsub" uses a two-step process for relating simple variable names like $$ia$$ to more complicated display forms such as $$i_a$$. It even relates the variable name $$pdelia$$ to the display form $$p_{del,{i_a}}$$
The notebooks pull the sym_helper file from its home on GitHub if needed.
You can look at the Trinket below, which will also grab sym_helper if needed. It uses the "nosub" version of the code because Trinket apparently, among other things, doesn't know how to make a subscript b print correctly...
- ↑ Peter Feldmann and Ronald A. Rohrer, "Proof of the Number of Independent Kirchhoff Equations in an Electrical Circuit." http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=00135739